This is the third part of the Julia on Google Compute Engine (GCE) series. The first entry discussed how to set up Julia on a standard GCE instance, and the second walked through working with Google Cloud Storage from within a Julia program. In this entry, we’ll be diving a little deeper into Julia, and talk about parallel processing.
Setting up your instance (reprise)
This is when your machine type matters a bit more. Now, GCE has basic, multi-core machine types, where the memory scales with the CPU count, but it has high memory, high CPU, and shared-core types as well. You want to pick the type that is most appropriate to your workload. For our experimentation, we’ll assume that you’re using a machine with four cores. To refresh your memory on how to create an instance through the Developers Console or the command line, take a look at the first Julia on GCE installation.
We want a multi-core machine so that we can take advantage of the easy parallel processing capabilities that Julia provides. There’s a more complex version where you can use multiple machines within a project to take care of simultaneous tasks, but that involves configuring networking, which we’ll set aside for now. In this example, each new thread will be farmed out to one of the cores on the virtual machine.
A simple parallel program in Julia
Before we get into anything terribly complex, let’s start with the basics. There are several functions in Julia that are specific to parallel computing:
remotecallremotecall_fetch@spawn@spawnat@everywhere@parallel
Note that the last four are prefaced by the @ symbol, indicating that they aren’t really functions; they are macros!
What’s the simplest possible program that we could write? How about a program that spawns some processes (we have four cores, after all), where each thread generates a number and reports it, along with the its identifier, to the command line? Let’s reduce the problem to one thread:
# get this process's identifier
id = myid()
# create variable, store random number
rand_num = rand(Int64)
@printf("process: %d int: %d", id, rand_num)
Easy. We get the id, generate the number, and output it. Now, let’s use some of Julia’s parallel computing-specific functions to farm this program out to multiple cores in a for loop:
for i=1:10:
# spawn the process
r = @spawn rand(Int64)
# print out the results
@printf("process: %d int: %d\n", r.where, fetch(r))
end
If we saved this in a file called parallel.jl, we’d tell Julia that we wanted it to parallelize over four cores by indicating it in the command line:
$ julia -p 4 parallel.jl
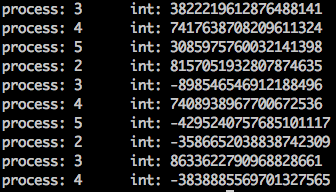
Once executed, you should see ten lines reporting their numbers, along with which core handled the generation:
Digging into the source of Julia, you’ll note that r, a RemoteRef, has three properties that you can access:
where: where the process is runningwhence: which process spawned this processid: identifier for the process
Try exploring where and whence with a little bit of @spawn inception (make sure you start it by typing julia -p 4 <filename>):
a = @spawn @spawn rand(Int64)
b = fetch(a)
@printf("a -> where: %d whence: %d\n", a.where, a.whence)
@printf("b -> where: %d whence: %d\n", b.where, b.whence)
@printf("resulting int: %d\n", fetch(b))
Your results might look something like this:
You can see that a’s where is equal to b’s whence, because that’s where b started.
Julia on Julia on Julia
I couldn’t resist – how meta could I make this blog entry? The Julia Set is a type of fractal that falls into the embarrassingly parallel problems category. Now, Martin Rupp already wrote a fantastic entry on constructing Julia Sets in Julia, so this will be based upon his introduction and we’ll tweak a couple things along the way.
We’re going to generate an 700px by 1000px image of a Julia Set. Now, because it’s embarrassingly parallel, we can calculate the shading of each pixel independently. The shading of each pixel depends on two things: an arbitrary complex number, and a complex number formed using the (x,y) values of the pixel. For the purposes of this example, let’s predefine our arbitrary complex number as C:
We’ll represent our second complex number as z, using the (x,y) values from the pixel in question:
The Julia function, the one used to calculate the value of a pixel, will look like this:
function julia(z, max_step, C)
for n = 1:max_step
if abs(z) > 2
return n-1
end
z = z^2 + C
end
return max_step
end
The parameters z and C are as we defined them above, and the max_step parameter dictates how high our values can go.
Now we’ll use this algorithm, in parallel, for every one of our pixels (700,000 of them, to be exact). However, we don’t have 700,000 processors at our disposal, so what we will do is split up the pixel ranges and give those ranges to separate processors to handle. It’s a perfect use for the distributed array! If we construct a distributed array, tell it what function to use and what its dimensions are, it will split up the work for us, using the indicated function:
julia_pix = DArray(<function>, (height, width))
We don’t yet have the function. Let’s define a function for it, and save it in julia_matrix.jl:
function parallel_julia(I)
# determine what section of the matrix we're calculating
yrange = I[1]
xrange = I[2]
array_slice = (size(yrange, 1), size(xrange, 1))
# construct interim matrix that we'll populate
matrix = Array(Uint8, array_slice)
# determine the lowest coordinates
min=xrange[1]
ymin=yrange[1]
# get the pixel values, convert to uint8
for x=xrange, y=yrange
pix = 256
z = complex((x-width/2)/(height/2), (y-height/2)/(height/2))
# find the value of the pixel using the above algorithm
for n = 1:256
if abs(z) > 2
pix = n-1
break
end
z = z^2 + C
end
matrix[y-ymin+1, x-xmin+1] = uint8(pix)
end
# done!
return matrix
end
Now, we’re partway there. We’ve got the algorithm to determine the pixel shading, the function to populate a section of the pixel matrix, but we’re missing the glue to pull it together and generate an image. For this, we’ll use a second file called julia_gen.jl:
# use the Images library
using Images
# load up our matrix calculation function
require("julia_matrix.jl")
# define some variable to be available to ALL processors
@everywhere width = 1000
@everywhere height = 700
@everywhere C = -0.8 - 0.156im
# construct our distributed array, passing in our function
# and the dimensions of the full pixel matrix
distributed_matrix = DArray(parallel_julia, (height, width))
# convert it to an array we can write our output file
pixel_matrix = convert(Array, distributed_matrix)
imwrite(pixel_matrix, "julia_set.png")
The results
Once you copy over your resulting julia_set.png image somewhere and take a look at it, it should look something like this:
If you change the value of C to:
you’ll get a very different set:
That’s it for parallel programming in Julia! I’ll be taking a little bit of a hiatus before my next entry on this topic.